During this past spring, we had a wonderful opportunity to partner with Scroll to research opcode pricing and the space complexity of different ways of posting proofs back to an L1. For those that don’t know, Scroll is a fast-growing start-up that specializes in developing a zkEVM. You can read more about what they’re building and our findings below.
A big thanks to Andy, Toghrul, Chris, and Daniel for helping us put this together!
Scroll is a unicorn in the web3 space working on an op-code compatible zkEVM. Opcodes are pre-defined instructions that the EVM can execute, such as arithmetic and logical operations, data movement, and storage access. Each opcode has a specific computational cost associated with it, which Ethereum uses to calculate the gas for a transaction. A zkEVM aims to extend the functionality of zkRollups to more complex transactions by generating validity proofs at each step of a contract’s execution. These proofs can be published back to the L1, allowing the chain to quickly verify the proof instead of re-executing each transaction. As a result, the L1 sees a significant increase in transaction throughput while maintaining the same level of security.
While there are other companies developing zkEVMs, Scroll is unique because their solution is op-code compatible. Because Ethereum was designed around security and decentralization, it isn’t easily compatible with the addition of Zero-Knowledge proofs. Generally, in order to make a zkEVM that can run all Ethereum contracts, developers have to sacrifice certain applications or developer tooling. For example, high-level zkEVMs that are only compatible with the underlying language (e.g. Solidity) mean that applications running on lower-level architecture cannot be carried over, such as debugging infrastructure. Scroll is aiming to build a zkEVM that is compatible with zkEVM opcodes, meaning that almost all existing EVM applications are compatible and can be quickly scaled using their zkEVM.
Opcode pricing is an important aspect of the Ethereum Virtual Machine (EVM) because it determines the cost of executing smart contracts on the Ethereum network. Each opcode has a gas cost associated with it, which is paid by the user who initiates the contract execution. The gas cost is calculated based on the computational resources required to execute the opcode. If the cost is too low, then the miners may face a negative operating income, resulting in no transactions being executed. Conversely, if the cost is too high, users are more hesitant to use the chain.
Some opcodes are cheaper than others. Nowadays, gas pricing is also multidimensional by considering the size, complexity, and priority of transactions. By incorporating opcode pricing into a multidimensional fee market, blockchain systems can provide more granular control over transaction fees and incentivize developers to optimize their code and minimize gas consumption. This can have implications for developers who are building decentralized applications (dApps) on top of Ethereum, as they need to consider the gas costs of their contracts when designing them.
This is especially challenging for Scroll because they have the proving cost as an additional layer to worry about. Internally, a zero-knowledge proof is generated by a series of complex circuits and rows for each op-code encountered, and there’s a high variance in the cost per opcode. Because a contract might behave differently based on the current state of the blockchain, there isn’t a way to determine the proving cost without actually running the transaction (i.e. the cost is unpredictable).
Another challenge that Scroll faced was deciding whether to publish transaction data or state differences of their transaction back to the L1. Both can be used to reconstruct the status of the chain after all the transactions on the zkEVM have been processed, and it’s obvious that the type with more efficient state usage would be better and cheaper to use. Additionally, it’s also necessary to determine how often to post data back to the L1. There’s a need to balance the costs of constantly posting data and keeping the state as updated as possible.
This was where our biggest contribution occurred. Our research consisted of fuzzing representative ERC20 contracts to randomly make transactions between different parties. While doing so, we recorded the size in bytes of the transaction data and state changes over a long period of time.
We could easily retrieve the transaction data using web3 libraries in Javascript, but state changes were more difficult. Internally, state changes are represented by changes in the nodes of Ethereum’s backing data structure: the Merkle Trie. In order to collect data on the size of the state changes, we modified the Go-Ethereum codebase found here: https://github.com/ethereum/go-ethereum to internally record the size of nodes touched by each transaction.
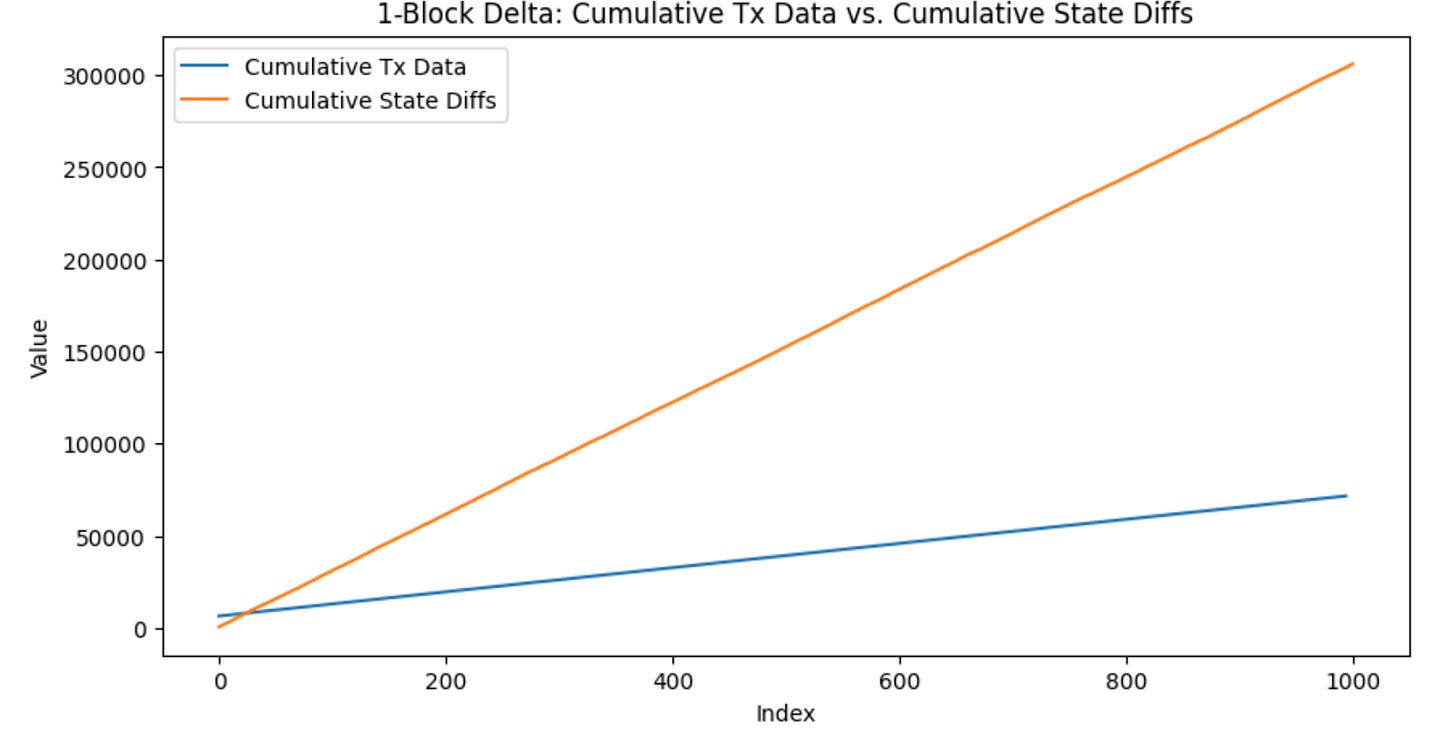
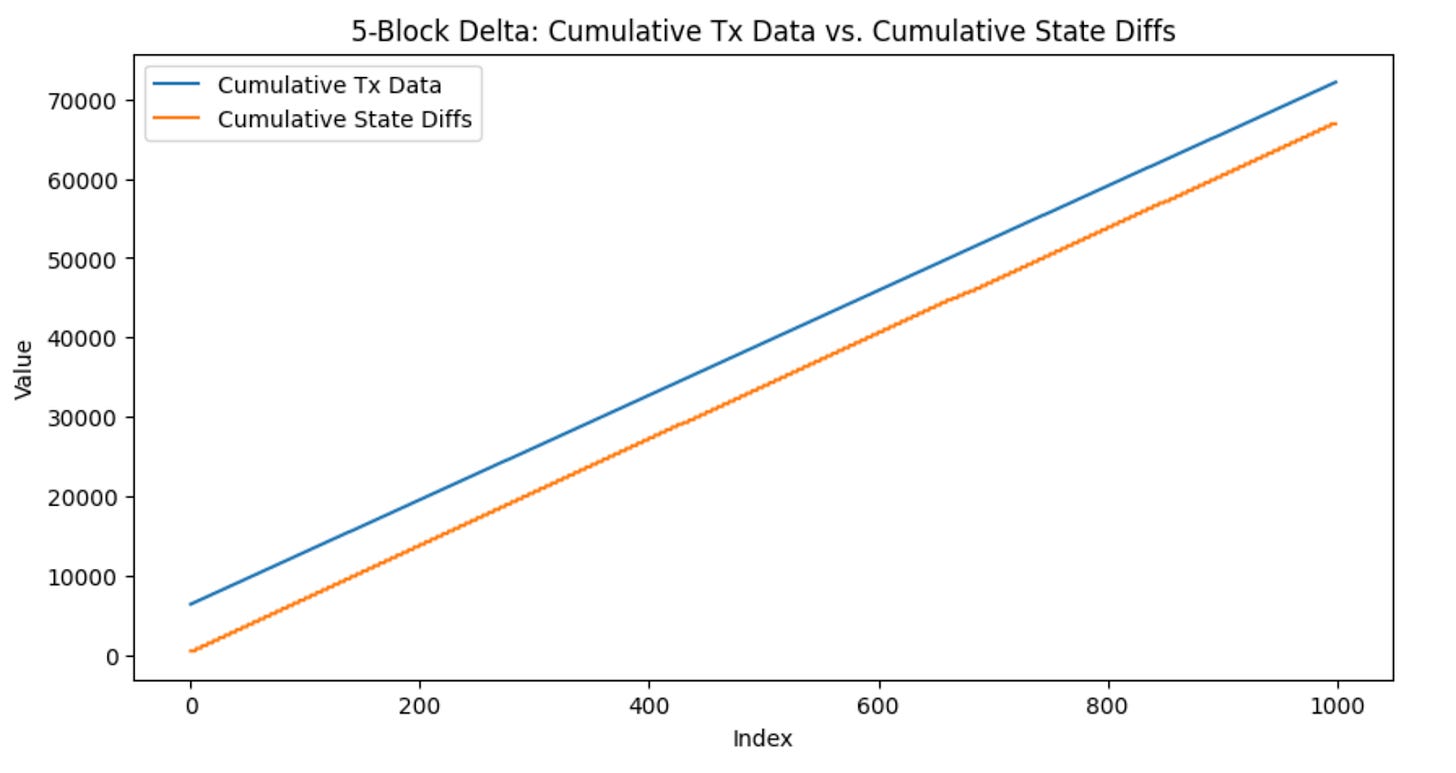
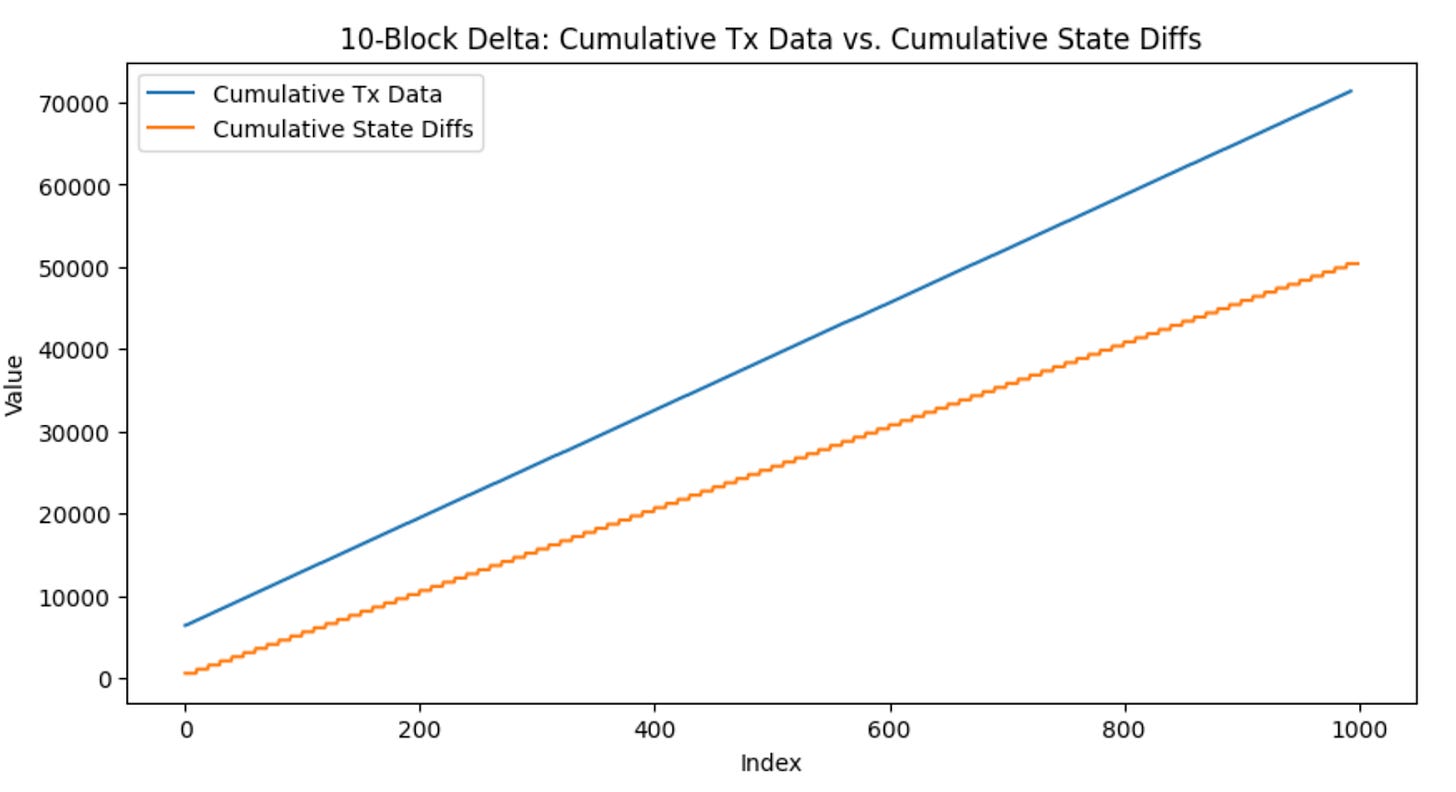
We also wanted to keep track of the number of state changes over many blocks. Specifically, we tested 1 block, 5 block, and 10 block intervals. To do this, we maintained a set of global “dirty” nodes (nodes that have been touched by a transaction), and we added or subtracted their size depending on if they were updated in a block. As a result, by varying the number of blocks in which we wanted to post transaction data, we were able to see the size of the cumulative state changes and the number of cumulative nodes touched. This data was written to a csv file in our own Geth codebase.
The two files that we touched were statedb.go located in core/state and nodeset.go located in the trie folder.
All of our changes in statedb.go lie in the Commit() function. The relevant variables are globalNodes, globalSize, counter, BLOCK_DELTA, and nodeSizes.
globalNodes is a redundant structure but allows us to utilize functions inside the nodeset.go file, where our other modifications were made.
globalSize keeps track of the cumulative size of the state changes. This is what gets posted back to the L1 after BLOCK_DELTA number of blocks.
counter keeps track of when we need to post back to the L1.
BLOCK_DELTA is a constant that determines how often data is posted back to the L1.
nodeSizes stores a mapping of the memory address of a node to the size of that node. When we touch a new node for the first time, we add it to this mapping. When we touch a node that has already been touched, we update its value in the mapping. This way, we only publish the most recent change to each node back to the L1, with no redundancy.
Inside the Commit() function, the relevant changes start on line 1121. globalNodes.Combine() combines our set of touched nodes with the set of nodes touched on this block. Combine() returns the new cumulative size, so we update the globalSize accordingly and increment the counter.
Every BLOCK_DELTA interval, we write the globalSize back to the L1 (a file, in this case). We then reset the globalSize, globalNodes, and the nodeSizes (set of nodes touched becomes empty).
At a high level, nodeset.go defines the functions you can call on nodes or sets of nodes that are updated in the trie. This is important because these are the same objects we need to post back to the L1 to represent a state change.
We modify the NodeSet structure to store a mapping of all the nodes that have been touched, keyed by their memory address. Fortunately, there are already functions that get called when a node is touched: markUpdated() and markDeleted(). We modify these functions to also update our mapping when a node is touched. There is old functionality inside the function that also keeps track of the totalSize per NodeSet. This isn’t necessary with the new way in which we collect data, but could be useful for other purposes, so we decided not to remove it.
We needed a way to merge the dirty nodes that a NodeSet object contains with the global set of nodes that have been touched, while also keeping track of their size. The Combine() function on line 323 handles this. It iterates through all the dirty nodes of the block and checks if they have been touched or not, updating the cumulative size passed in accordingly. Since we care about the size at the end, this is what we return. It is also what globalSize gets updated to in statedb.go.
Here were some of the findings that we discovered:
We observed that the size of the transaction data aligned with what one would intuitively reason. The first transaction, the contract deployment, took up the most amount of bytes (~100x) more bytes due to having to supply the contract bytecode in the calldata. Afterwards, each ERC20 transaction took the same number of bytes in calldata. This also made sense, since the amount of data needed for an ERC20 transaction is always the recipient and the value transferred.
Interestingly, the size of the state changes (even for contract deployment) remained pretty similar in value as well, with small fluctuations here and there. However, it was much more expensive than a typical non-contract creating transaction’s calldata. This highlighted the advantages and disadvantages of using state changes: the state changes will not blow up in size even for transactions with a lot of calldata, but will be much more expensive if you’re comparing state changes to just one transaction.
We saw that when increasing the number of blocks before submitting state changes back to the chain, the state changes only went up slightly in size, indicating that transactions within a block touch the same state often. Additionally, the size of the state changes seemed to converge to a single value with the more blocks we included. This means that as we increase the number blocks between which we post state differences, there is a decrease in the size that is being posted in data for state differences.
In the future, our study should be extended to more complex contracts within different verticals (i.e Multi Layered contracts, upgradable contracts, etc.). This would allow for a more comprehensive representation of blockchain data, resulting in a more accurate simulation and data collection. Moreover, to analyze the opcode pricing to the best of our knowledge, we should consider doing a multi dimensional study that takes into account different opcode specific inputs, gas consumption over time, different network conditions— and finding relationships between all the different variables to somehow find a model that allows for the most efficient pricing, ultimately resulting in an optimal ratio between computational power and opcode pricing.